Арбузный ломтик по средам № 142
Шестое тело
| |
— Здравствуйте, — на всякий случай сказал Петропавел, с
восхищением глядя на девушку.
— Виделись уже, — улыбнулась та и протянула ему руку: -
Пластилин Мира. — Петропавел пожал руку. Рука осталась у него
в кулаке. С ужасом и отвращением он бросил руку на пол. Девушка подняла ее и приставила на прежнее место:
— Фу, неаккуратный какой! Осторожнее надо…
Евгений Васильевич Клюев. Между двух стульев |
В прошлой колонке, посвященной орнаментам, мы говорили о замощении плоскости правильными многоугольниками. В каждой точке, вершине орнамента, при замощении все многоугольники складывались без зазоров и нахлестов. А что, если мы уберем один из многоугольников и соединим границы пустого места? При этом фигура станет не плоской, а выпуклой. Например, из четырех квадратов, заполняющих плоскость вокруг вершины, удалим один и совместим ребра в зоне пустоты. Получим половинку куба. Таким приемом мы сможем получать правильные многогранники, то есть выпуклые тела, все грани которых одинаковые правильные многоугольники.
Можете проделать мысленно эти эксперименты со всеми многоугольниками, которыми мы замостили плоскость. Если трудно мысленно — то бумага и ножницы помогут развить воображение. Лучшей темы для занятий с детьми вообще не найти. Я в детстве часто ковырялся с такими штуками, каждый раз поражаясь мудрости и гармоничности устройства мира. Помните, что в плоской вершине сходились шесть треугольников? Оставьте три и сложите — получим заготовку для пирамиды или тетраэдра. Если оставить в вершине четыре треугольника — придем к октаэдру. Если пять — к икосаэдру, красивейшей и волнующей фигуре. Можно даже сразу узнать количество вершин будущего многогранника. Угол, которого не хватает в каждой вершине до плоского заполнения, назовем дефицитом. Так вот — сумма всех дефицитов всегда равна 720 градусов. Например, если в вершине пять треугольников, не хватает одного, и дефицит равен его углу при вершине или 60 градусов. Делим 720 на 60 — получаем 12 вершин у икосаэдра.
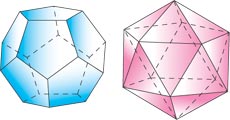
Самое удивительное то, что таких тел, правильных многогранников, всего пять. Тетраэдр, октаэдр, икосаэдр, куб и додекаэдр. Известны они с древности и называются Платоновыми телами. Тот факт, что больше пяти Платоновых тел быть не может, казался мне в детстве просто ошибкой. Ну не открыли пока. Вдруг завтра кто-то найдет новое тело — что тогда скажут математики? Это сподвигало меня на разные вычисления, было исписано и изрезано много бумаги. Шестое Платоново тело не найдено. Не может его быть. Давно уже это понял. Но где-то далеко внутри осталась тлеющей искоркой надежда — а вдруг?
Вопросы для тех, что что-то понял. Сколько вершин у додекаэдра? Какое минимальное количество красок нужно для раскраски каждого тела с учетом того, чтобы смежные грани не были одного цвета? У какого из Платоновых тел можно обойти все ребра не отрываясь и не проходя по ним дважды?
Если у каждого из пяти Платоновых тел вместо вершин вдруг станут грани, а вместо граней — вершины, то одно из тел останется самим собою, какое именно?
21.03.2007
Теги: задачки
занимательные модели
|
