Замечательные червяки

Знакомо ли вам состояние, когда виденная однажды идея не оставляет и заставляет периодически к ней возвращаться? Так было (и есть), например, с играми «Жизнь» и «Козлики и волки». То же и с так называемыми «Червяками профессора Брауна». Это я так назвал эту модель в честь выдумавшего ее австралийского математика Пола Брауна, о котором рассказала «Компьютерра» четырехлетней давности.

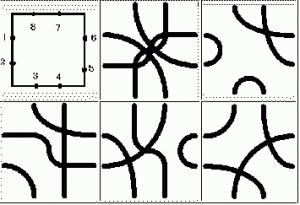
Идея профессора-художника заключается в следующем. На каждой стороне квадрата берутся две точки и соединяются, попарно, четырьмя линиями. Если такими квадратами замостить плоскость — то вы ахнете от восторга! Даже сами статичные картинки вариантов красивы, а уж о движущихся на экране живых бурлящих соединениях и говорить нечего. Посмотрите, как это выполнено на страничке Брауна, там же есть и статья о слиянии математики и искусства.

Сразу же возникает волнительный вопрос — сколько вариантов соединений в одном квадрате существует? Я насчитал 105 вариантов соединений без учетов поворотов и отражений; если кто-то меня поправит, буду признателен. Количество уникальных вариантов с учетом поворотов-отражений, естественно, намного меньше, жду соображений читателей. Идея не отпускает, пока не напишите программу и не наиграетесь с параметрами, причем сам процесс написания, кодирования, продумывания алгоритма необычайно приятен. Задав массив и начав его заполнять, вы столкнетесь с массой чудесных трудностей, например, если первая точка соединяется с пятой, то они обе выбывают из кандидатур для соединений с другими точками. Но, уверяю вас, затея стоит того. Невозможно не привести замечательную конструкцию, появившуюся в программе: a(a(i)) = i. Она красива сама по себе, не представляю, в какой еще задаче она могла бы появиться.

Еще хотелось бы, чтобы червяки не перерисовывались, а плавно переползали из одного положения в другое. Мне этого добиться не удалось. А знакомый по переписке Андрей прислал такую программу, можете с ней поиграть. Попытайтесь написать программу. Если вы из числа программистов, забывающих время и пространство, когда одолевает идея — то это для вас — подсядете надолго. И будете жалеть предыдущую бездарно прожитую без червяков жизнь.

Снова вернулся я к этой теме потому, что Михаил Кочеров написал просто замечательный скринсейвер с червяками. Настраивается цвет фона и червяков, толщина линий, размер квадрата и количество меняющихся квадратов. Мышку даю на отсечение — оторваться от заставки невозможно. Это не только завораживающая модель мышления, общественных, социальных, коммуникативных процессов, но и необычайно эмоциональная штука, непременно поднимающая настроение. Все подопытные отмечали положительное психологическое воздействие от разглядывания картинки (стрессы снимает, давление, близорукость… и начинает везти, даже если вы в это не верите — понаблюдайте за собой после установки программы). Не самые душевно толстокожие находят также эстетическую составляющую в этом перетекающем узоре. Ну и просто приятно глазеть на этих червяков, думая о чем-то своем.

«Использованная литература», то есть, по-новому, рекомендуемые ссылки:

• Первоисточник — червяки самого Пола Брауна.
• Статья «Четыре шага к новому искусству», часть 2 — о червяках, там есть и анимированная картинка.
• O программе Андрея.
• Статья «Визуализация информации», в ней тоже есть абзац о червяках.
• Скринсейвер (ZIP-архив, 106 Кбайт).

Задачи ломтика вытекают из текста.

1. Сколько же существует вариантов соединений точек в квадрате? И сколько вариантов останется, если считать полученные отражением и вращением одинаковыми?

2. Давно меня занимает идея выразить вид квадрата с линиями характеристическим числом, однозначно описывающим прохождение линий. Вроде простая задача, но ускользающая…