|
|
Арбузный ломтик по средам № 174
Красивые задачи по геометрии
| |
Парадокс, но если выясняется, что человек интеллектуально развит, много читает, слушает классическую музыку, то многие будут к нему относиться не иначе, как к проклятому ботанику, умнику и ужасно скучному человеку.
Из дневника Zabriskie |
Просто захотелось вспомнить красивые задачи, попадавшие в поле зрения. Знаю, что есть любители красивых задач, любители поковыряться с задачками и даже, самые утонченные, любители красивых условий геометрических задач. Задачи встречались в «Арбузном блоге», «Арбузном» и других форумах, в сообществах разных и на простых страничках бескрайней Сети. Спасибо всем авторам задач. Решения не привожу — прошу в комментарии в блоги, форумы, ЖЖ — адреса знаете. Рядом с истиной красотой все пояснения излишни, начинаем.
Концы нитки, продетой через кольцо, закреплены на концах А и В дощечки. Длина нити L больше расстояния АВ. Найти отрезки, на которые делится нитка свободно висящим кольцом при наклоне дощечки на угол ω от вертикали. Трением и весом нитки пренебречь.
Имеется в наличии: картина, веревка, два гвоздя, вбитых в стену.
Нужно: повесить картину на стенку так, чтобы при вытаскивании любого из гвоздей она падала.
Кусок сыра имеет вид прямоугольного параллелепипеда 10×13×14. От него 10 раз отрезали полоски толщины 1 (каждая полоска была параллельна одной из граней параллелепипеда, но разные полоски могли быть параллельны разным граням). Какой наибольший объем может быть у оставшегося куска?
Гипотенуза прямоугольного треугольника (в американском стандартном экзамене) — 10 дюймов, а опущенная на неё высота — 6 дюймов. Найти площадь треугольника.
С этой задачей американские школьники успешно справлялись 10 лет, но потом приехали из Москвы русские школьники, и ни один эту задачу решить, как американские школьники (дававшие ответ 30 квадратных дюймов), не мог. Почему?
Есть два куба с ребром длиной 5 м. Первый разрезан на кубики, ребро каждого из которых равно 2 см. Эти кубики выложили в один сплошной ряд. Второй разрезан на кубики с ребром в 1 см. и эти кубики тоже выложены в ряд. От какого куба ряд длиннее и на сколько?
Представьте, что вы попали на планету, имеющую форму куриного яйца. В какой точке планеты сила тяжести будет максимальной?
Какая из планет в среднем дальше от Плутона — Меркурий или Марс, если известно, что радиус орбиты Марса намного больше радиуса орбиты Меркурия?
Когда двое несут диван по лестнице (только что соседи тащили) — кому тяжелее — верхнему или нижнему тащильщику?
Так никто и не решил простую задачу: Можно ли только линейкой найти центр имеющейся окружности?
Площадь треугольника, один из углов которого равен разности двух других, равна площади квадрата, сторона которого совпадает с одной из сторон этого треугольника. Найти углы данного треугольника.
Имеются две круглые башни одинаковой высоты, но разного диаметра. Вокруг каждой из них идет винтовая лестница, причем угол наклона каждой из лестниц к горизонту везде постоянен и одинаков для обеих башен. По какой из лестниц путь к верхней площадке башни длиннее: по той, у которой диаметр больше, или наоборот?
На какое наибольшее число частей могут разделить пространство поверхность куба и сфера?
На сторонах BC и CD квадрата ABCD построены внешним образом правильные треугольники BCK и DCL. Докажите, что треугольник AKL — правильный.
У двух следующих задач красота условия соперничает с неочевидностью результата и сложностью «зацепки» за простой на первый взгляд сюжет. Выложил Дин Гиор в «Арбузном форуме».
Эллипс с эксцентриситетом ε установили на наклонную плоскость с уклоном ω так, что его большая полуось параллельна этой плоскости. Покатится ли эллипс? Или только качнется? При каком значении ω эллипс покатится?
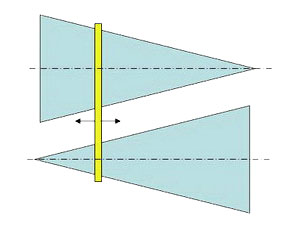
Всем знакомый с детства вариатор. Смотрите рисунок. Два конических вала, ремень. Изменяется ли натяжение ремня при его перемещении? Если да, то какой формы должны быть валы (вместо конических), чтобы натяжение (соответственно и длина) ремня оставалось постоянным?
19.11.2008
Теги: геометрия
задачки
|
Ваш отзыв автору
|
|
|
