|
|
Арбузный ломтик по средам № 81
Тростинки в колодце
| |
Ему казалось — на трубе
Увидел он Слона.
Он посмотрел — то был Чепец,
Что вышила жена.
И он сказал: «Я в первый раз
Узнал, как жизнь сложна».
Люис Кэрролл. «Песня Безумного Садовника» из романа «Сильви и Бруно» в переводе Д. Г. Орловской |
 Однажды в «Арбузном форуме» выложили заурядную, казалось бы, геометрическую задачу про трапецию. Завсегдатаи принялись, обмениваясь, как обычно, репликами и озарениями, ее решать, вовлекая новых участников и открывая красивую историю задачи. Историю эту начинали не менее чем с Древнего Египта, это было заманчиво и романтично и, главное, отсекало методы решения, заведомо не известные древним египтянам.
Однажды в «Арбузном форуме» выложили заурядную, казалось бы, геометрическую задачу про трапецию. Завсегдатаи принялись, обмениваясь, как обычно, репликами и озарениями, ее решать, вовлекая новых участников и открывая красивую историю задачи. Историю эту начинали не менее чем с Древнего Египта, это было заманчиво и романтично и, главное, отсекало методы решения, заведомо не известные древним египтянам.
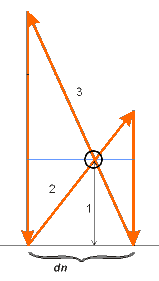
Итак, условие задачи. В цилиндрический колодец опущены две тростинки длиной два метра и три метра так, что они пересекались и точка пересечения находится на высоте одного метра от дна. Найти диаметр колодца. Пояснения — нижние концы тростинок лежат на дне в противоположных концах диаметра колодца, а верхние концы опираются на стены колодца. Еще говориться в условии, что уровень воды проходит как раз через точку пересечения тростинок, но это для красоты условия, к решению отношения не имеет. Если кого-то смущают метры в качестве единиц измерения, можете заменить их на локти или любые меры, используемые в Древнем Египте.
Вообще о древнеегипетских корнях задачи мы узнаем из рассказа известного фантаста Александра Казанцева «Колодец Лотоса». Претендентов на пост жреца замуровывали, сообщив условие задачи, и единственным условием выхода была передача в специальное отверстие камня с нацарапанным на нем ответом. При правильном ответе узник выпускался в сане жреца бога Ра.
Нам трудно сейчас проверить древнеегипетские легенды, зато есть более достоверная информация. Виртуальный знакомый Игорь, отслеживающий все, что связано с этой задачей, пишет: «Впервые, насколько мне известно, она была опубликована в 1966 г. в журнале „Наука и Жизнь“, № 1. В редакцию пошли письма, через два года было сделано обобщение присланных попыток с выводом: удовлетворяющего решения нет. В 80-ые годы, в период бурного освоения программируемых калькуляторов, журнал вновь возвращается к этой задаче. Делаются новые попытки и, наконец, в 1984 г. был опубликован алгоритм решения уравнения методом итерации с помощью калькулятора. Началось соревнование, кто быстрее получит вожделенное число».
В чем же суть проблемы? В том, что задача решается тремя способами:
— приводится к уравнению четвертой степени, решить которое очень даже непросто;
— через обратные тригонометрические функции в виде многоэтажного замысловатого уравнения;
— итерационным приближением, столь доступным с появлением Бейсика или Excel.
Но эти методы не были известны в древности, поэтому энтузиасты уже много лет тратят ночи (и даже рабочее время, только тсс) на поиски изящного геометрического решения. На первый взгляд так все просто — провести дополнительные построения, рассмотреть подобные треугольники и… И пока никак.
Призываю отбросить суету и попытаться найти простое красивое решение. Это будет лучший из всех вариантов наполнения жизни смыслом.
Для разминки можете поискать в Сети «Колодец лотоса» или «Тростинки в колодце», но сначала рекомендую познакомиться с дискуссией на «Абузном форуме», там же есть и самые толковые ссылки по существу вопроса. Когда найдете простое решение и прославитесь — не забудьте сослаться на «Информационный бум».
Обсудить текст и задачу можно в моем журнале.
02.11.2005
Теги: задачки
|
Ваш отзыв автору
|
|
|
