Цветы, пропеллеры, вертушки

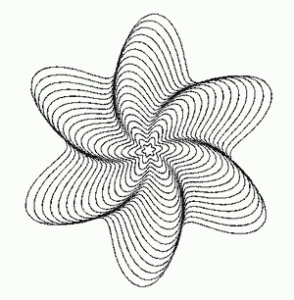
Самые частые и затягивающие забавы — это рисование всяких кривых в полярных координатах. Начните, например, с уравнения R = R₀sinφ — даже без запуска программы ясно (при минимальных знаниях тригонометрии, конечно), что мы получим два лепестка, так как синус дважды равен нулю — в начале цикла при φ = 0 и при φ = 180°. А при φ = 90° и φ = 270° получим максимум и минимум соответственно. Все — больше никаких особых знаний не надо для продолжения захватывающих опытов. Первое, что просится — попробовать ввести множитель n для угла: R = R₀sin(nφ). Заранее предскажем, что при n = 2 нарисуется цветок с четырьмя лепестками, при n = 3 — с шестью и так далее. Или наоборот, взять n = 0,5 — нарисуется однолепестковая похожая на сердечко фигура, так и называемая из-за этого «кардиоидой». Кардиоида является частным случаем замечательной кривой — «улитки Паскаля», о ее занимательных свойствах расскажем в следующий раз. А что будет при n = 1,5 или даже при n = 1,25? Тут рассуждения не помогут — надо начинать рисовать, пробовать менять n и каждый раз удивляться полученной фигуре.

Когда освоитесь — следующий шаг. R = R₁ − R₀sinφ — то есть, мы из окружности вычитаем наши лепестки. Рассмотрите разные соотношения R₁ и R₀. Это довольно занятно. Постепенно вы научитесь заранее предсказывать вид полученной линии при любых параметрах уравнения R₁ − R₀sin(nφ). Развивать забаву можно в разных направлениях; один из любимых вариантов — добавить еще слагаемых с разными значениями параметров: R₁ − R₀sin(nφ) + R₂sin(mφ) и получить цветки сирени, листики, розочки и прочие красивости. А еще можно возводить sin(nφ) в какую-нибудь степень (целую, конечно), что позволит «заострить» лепестки, причем важна четность этого показателя — при четном показателе «отрицательные» лепестки становятся «положительными», стоит попробовать! Но мы идем дальше в выбранном направлении — создаем еще один внешний цикл и меняем в нем радиус. Получаем семейство лепестков, растущих из одного центра. И тут делаем небольшую корректировочку, в которой, собственно и состоит вся изюминка. В аргумент синуса добавляем (с коэффициентом, естественно) текущий радиус! Это позволяет каждый следующий слой немного закручивать относительно предыдущего, что и порождает не просто лепестки, а пропеллеры, крыльчатки, улитки прочие чудеса — в зависимости от параметров. И дает простор для бесконечных опытов. Посмотрите мою колекцию. Присылайте красивые рисунки и алгоритмы или выкладывайте на своих страничках в Сети. Вряд ли у вас есть на примете более достойное занятие.

Задача ломтика.

На доске написаны все целые числа от 1 до 1000. Алиса и Громозека по очереди вычеркивают какое-нибудь число, а затем все его делители. Проигрывает тот, кому нечего вычеркивать. Начинает, допустим, Алиса. Кто выиграет при правильной игре?