Глобус плоского мира

После того, как была опубликована предыдущая колонка о плоском мире, я получил несколько писем, в которых читатели предсказывали ход моих мыслей в последующих колонках. «Все ясно, — писали читатели, — в следующих колонках вы подведете нас к мысли о том, что мир котором мы живет, вовсе не трех, четырех, пяти или даже шестимерный».

Полноте, господа! Неужто я начал цикл этих колонок только ради того, чтобы еще раз провозгласить банальность, истрепанную многими поколениями писателей фантастов!

Так что не гадайте, а давайте-ка вернемся назад в наш дивный плоский мир и посмотрим, что там творится.

Двухмерные геометры — в растерянности, они никак не могут понять, почему как только диаметр окружности в их мире достигает достаточно большой величины, она сходит с ума, и вместо того, чтобы расти, начинает уменьшаться.

Но — в любом плоском мире очень развита геометрия. Им там ничего другого не остается, других наук ведь там почти не существует. А потому геометры плоского мира конечно смогли бы втиснуть объемный шар в рамки своего плоского мира.

Ведь известно что любую объемную фигуру можно «развернуть» на плоскость, и наоборот. Подобно тому, как плоский рисунок карты натягивается на объемный глобус.

Так что в конце концов геометры плоского мира худо бедно, наверное, создали бы модель шара на плоскости, и выглядела бы эта развертка точь-в-точь, как выкройка нашего глобуса.

Примерно — вот так.

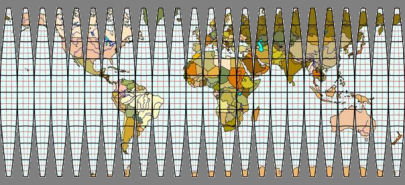
Как ни парадоксально, эта модель идеально описывала бы все происходящее в плоском мире и дала бы ответ на все загадки. При помощи этой модели плоские геометры представили бы объемный трехмерный мир как два плоских мира, один из который видимый (то, что на «развертке») и невидимый (серый), который тоже, очевидно, существует, но увидеть который нельзя.

И все отклонения от стандартной геометрии объяснялись бы просто тем, что часть фигуры попала в невидимый мир и исчезла в нем. Окружность по мере роста диаметра не уменьшается, она растет, как и должна расти, но при этом часть ее попадает в невидимый мир, вот она и кажется меньше.

Разумеется живые двухмерные существа тоже не могут попасть в невидимый мир. Достигнув границы мира видимого, они просто каким-то неведомым способом по какому-то столь же невидимому тоннелю мгновенно оказываются на противоположной границе видимого мира, даже не заметив, что переместились.

«Ерунда! Бред!» — Скажете вы.

Возможно. Но чем, скажите это отличается от «туннелирование частиц», «кротовых нор» и прочих занятных вещей, которыми развлекаются наши вполне объемные физики.

22.12.2010

Теги: окружность туннель шар