|
|
Арбузный ломтик по средам № 148
При чем тут автоматы?
| |
Слон-живописец написал пейзаж,
Но раньше, чем послать его на вернисаж,
Он пригласил друзей взглянуть на полотно:
Что, если вдруг не удалось оно?
С. Михалков. Слон-живописец |
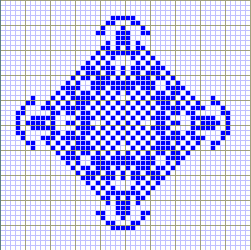Автоматы не причем, или почти не причем, просто устоялось название «Клеточные автоматы» (КА) как дословная калька с английского cellular automata. Впрочем, название не так уж важно, все привыкли, при ближайшем рассмотрении можно найти и автомат. КА — это набор ячеек, каждая из которых может быть в нескольких состояниях, связанных каким-либо законом. В самом простом случае ячейки это квадратные поля шахматной доски, состояния ячейки соответствуют какому-либо цвету, а уж законы взаимодействия ограничены только нашей фантазией. Даже этой вступительной информации достаточно, чтобы любители всяких программических развлечений накидали программку и получили бы удовольствие от возникающих узоров.
Напомню основные интересные с точки зрения компьютерных развлечений разделы КА. Это «тьюрмиты» (название от машины Тьюринга), у них в алгоритме заложено развитите, в том числе движение по плоскости и изменение цвета. Самым простым и самым популярным примером КА является игра «Жизнь», в ней у ячеек всего два состояния и правила развития просты и изящны. Появились также сообщения о вероятностных КА, позволяющих моделировать нелинейные динамические системы вроде погоды, социальных процессов, энтропии и так далее. Вот зубодробительная цитата для любителей точных формулировок: «…можно применять ВКА к решению таких задач, как: влияние флуктуаций на динамические режимы нелинейных систем; образование структур Тьюринга; влияние гидродинамических мод на поведение химических нелинейных систем (эффекты перемешивания); бифуркационное изменение динамического режима сложных систем в условиях ограниченной подвижности или низкой пространственной размерности; описание химических систем в микроэмульсиях».
Но нас больше интересует КА с точки зрения программных развлечений. Создаем поле — он же двумерный массив, назначаем цвет ячеек в зависимости от состояния, а само состояние — в зависимости от состояния соседних ячеек. Естественно, что надо задействовать «возмутителей» — одну или несколько точек с «ненулевым» состоянием — источники инфекции или центры кристаллизации и запустить процесс. Сразу он может не пойдет, стоит поиграть коэффициентами, позже все силы будут уходить на «усмирение» разбушевавшейся стихии. Какие направления совершенствования? Сделать процесс трехмерным, появляется проблема видимости (первый план зарывает задний) и рисования аксонометрии, будем считать, что эти задачи вам уже по плечу. Еще напрашивается переход с поля с квадратными ячейками на поле с шестиугольными ячейками. Делается довольно просто — каждый четный ряд сдвигается на полшага по горизонтали и получаем шестиугольную структуру, у каждой ячейки шесть соседей. Правда с отслеживанием соседей придется повозиться, но хлопоты будут вознаграждены полученным на экране процессом.
А вот еще идея, которая, собственно, и дала повод к написанию колонки. Автор блога Sergey Lymar рассказал о КА в котором ячейки могут принимать не фиксированные, а непрерывные значения. Это неожиданное расширение теории КА позволяет запустить новые, невиданные ранее процессы. Например, тригонометрические зависимости от состояния соседних ячеек. Или даже арккосинус от синуса суммы состояний соседей, что дает очень красивый узор. И не просто узор — можно посмотреть его «кипение-бурление» в реальном времени. Куда двигаться дальше? Можно довести идею до абсурда — попытаться уйти от фиксированных ячеек, рассматривать плоскость как непрерывную, с плавным изменением характеристик. Тут две трудности. Первая — не известно, как брать тогда состояния соседей — все равно придется рассматривать какие-то локальные области. Вторая, технологическая — при выводе на экран все равно оперируем пикселями, совсем уйти от дискретности не получится. Впрочем, обе трудности преодолимые, если задаться некоторыми допущениями. Что получим? Что-то в виде аттрактора. Это опять сложный термин, об этом как-нибудь в следующий раз.
Ссылки
Оказывается, уже была колонка о КА «Экранные эпидемии», склероз, наверное. Но содержание не повторяется, можете проверить.
Еще колонка — «Есть ли у вас жизнь?».
Блог Sergey Lymar — там уже новые чудеса появились.
Cтатья Константина Кнопа о Тьюрмитах в Компьютерре, 1998 год.
07.06.2007
Теги: игры
клеточные автоматы
тьюрмиты
|
Ваш отзыв автору
|
|
|
